Research

Computation, evolution, and immunity
The DeWitt lab is committed to advancing science with quantitative models and computational tools. Broadly, we’re interested in applied probabilistic and dynamical modeling, statistical inference, optimization, and machine learning, all grounded by questions about evolving biological systems. In addition to innovating theoretical and computational methods, we work closely with domain experts and experimentalists to design and analyze data and discover new biology. We work at the interface between quantitative sciences and biology, and enjoy interdisciplinary collaborations and inclusive scientific discourse.
Quantitative immunology

A key direction is to synthesize dynamical evolutionary modeling with deep representation learning to predict and control the adaptive immune system, and to understand host-virus co-evolution. We aim to clarify how immune memories are encoded and how systemic responses emerge, both in terms of rapid evolution in immune receptor repertoires and co-evolution with rapidly evolving pathogens. Adaptive immunity is an ideal setting to think about the function of evolving systems. There is considerable scope for sequence data-driven studies of evolutionary mechanisms in this setting.
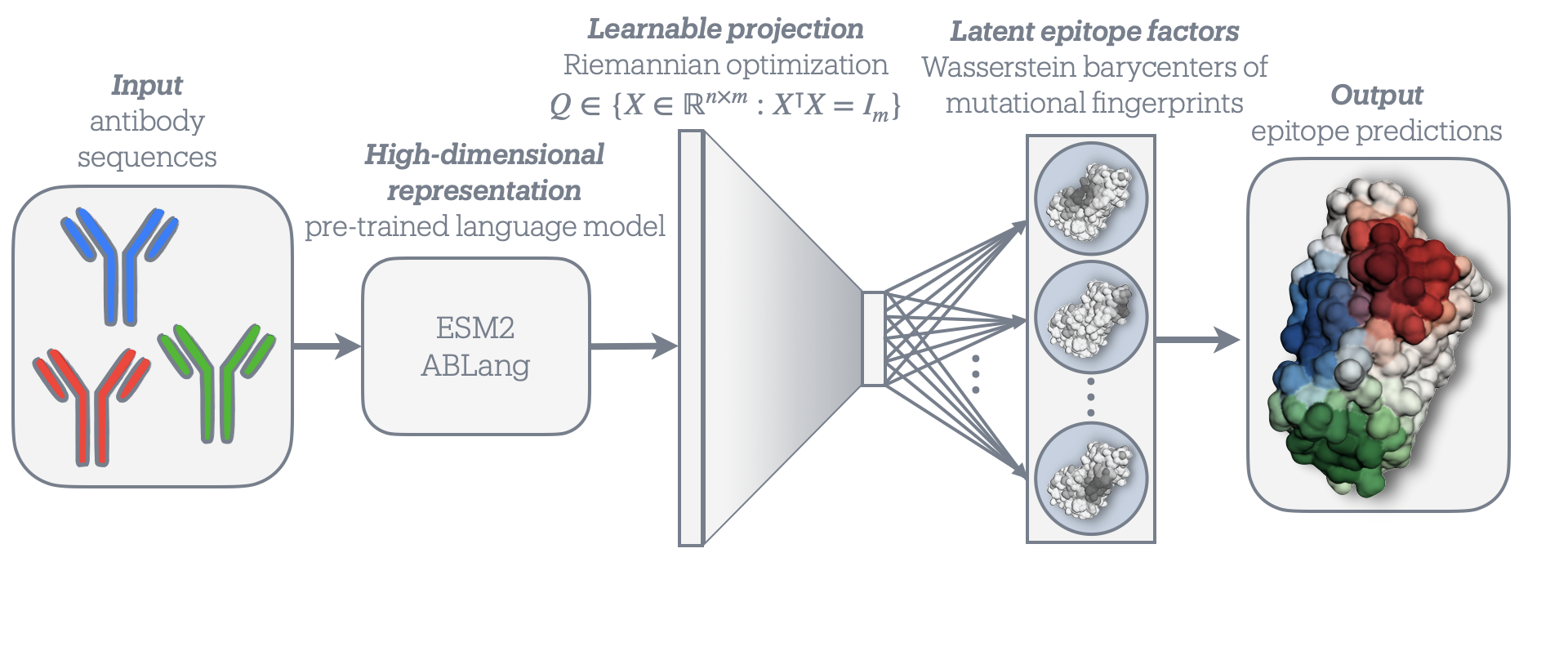
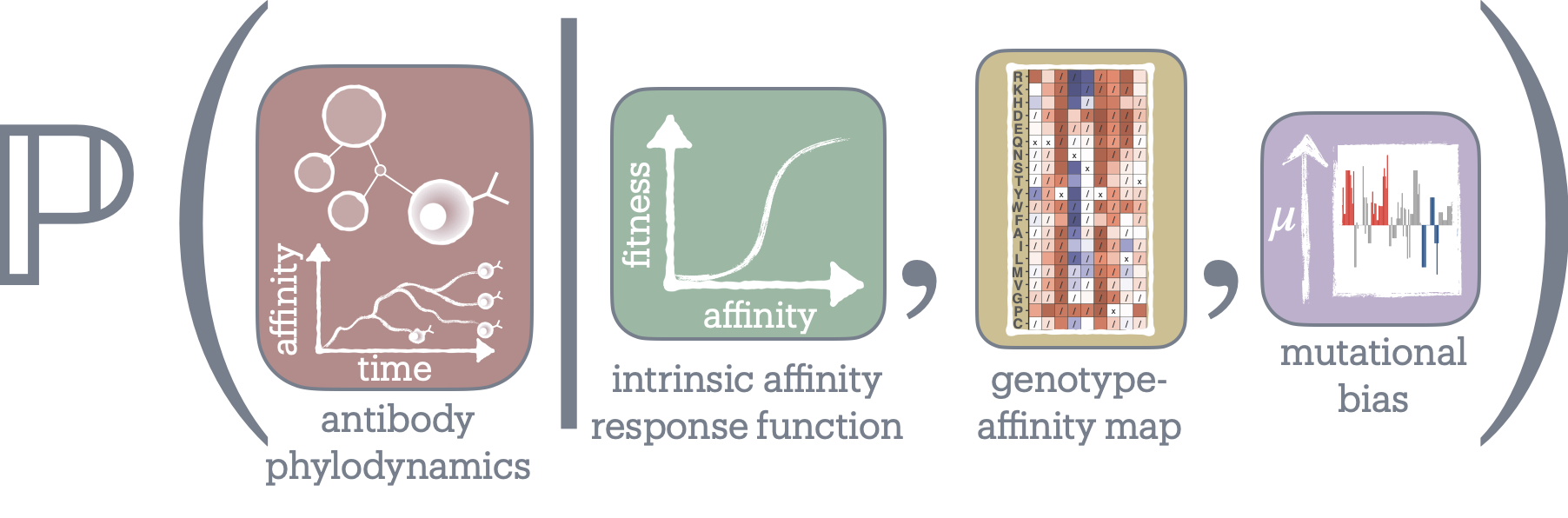
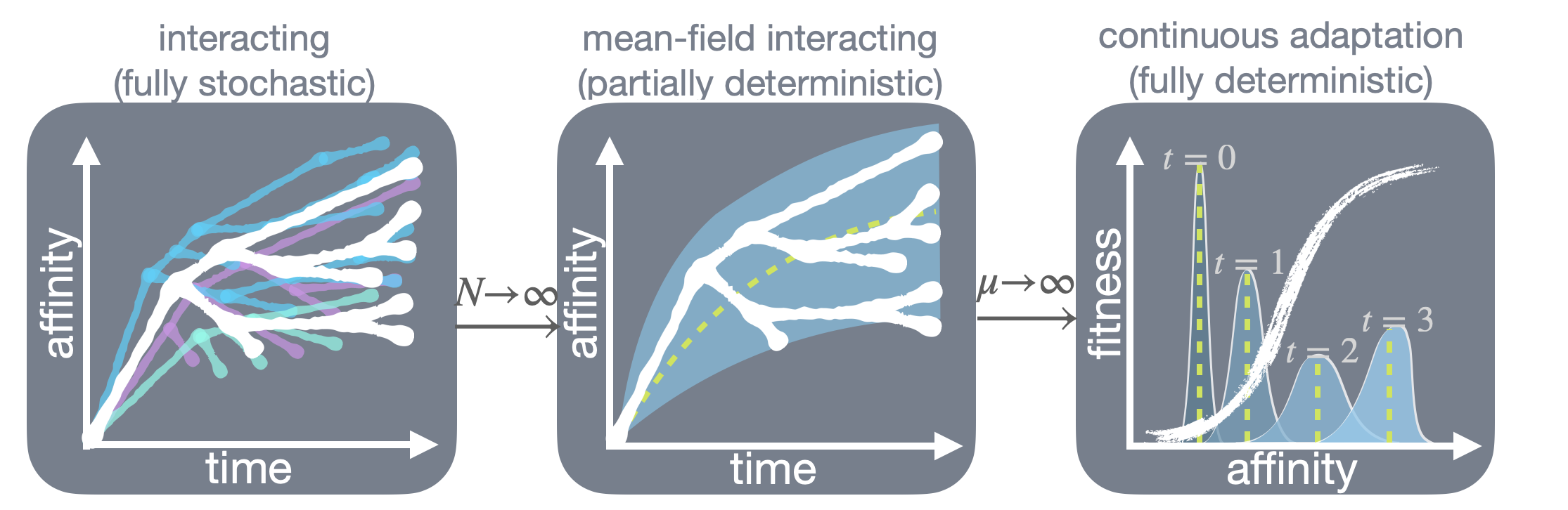
Evolutionary dynamics

We are also interested in theoretical and computational topics in evolutionary dynamics, including mean-field approaches to interacting tree processes, ill-posed inverse problems, sparse optimization, and graph-based machine-learning architectures, which have the potential to accommodate complex biological processes. Many problems in evolutionary inference—on time scales ranging from phylogenetic to population genetic to somatic—are amenable to these computational techniques when framed appropriately. We aim to understand evolutionary dynamics in complex evolutionary settings—with interactions and multi-scale adaptation—that are out of reach for standard models.